Method of Mathematical Physics by Mr. Muhammad Usman Hamid
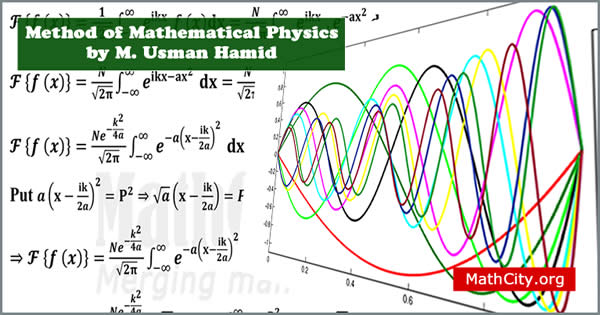
Method of Mathematical Physics is an area of mathematics concerned with the application of mathematical methods to physics problems. Mathematical techniques for statistical mechanics, quantum mechanics, and classical mechanics are all included in this large field.
The notes provides a foundation to solve PDE's, ODE's, IE's with special emphasis on wave, heat and Laplace equations, formulation and some theory of these equations are also intended. These notes are send by Mr. Anwar Khan and written by M. Usman Hamid. We are really very thankful to him for providing these notes and appreciates his effort to publish these notes on MathCity.org
Summary
- Name: Method of Mathematical Physics(MMP)
- Provider:Mr. Muhammad Usman Hamid
- Pages: 250 pages
- Format: PDF
- Size: 4.89 MB
- Category: Mathematical Method
What is in the notes?
In this section, the main heading are given below.
- Difference equation
- Differential equation
- Ordinary differential equation
- Partial differential equation
- Homogeneous differential equation
- Non-homogeneous differential equation
- The order of a partial differential equation
- The degree of a partial differential equation
- Linear partial differential equation
- Non-linear partial differential equation
- Initial conditions
- Initial value problem
- Boundry conditions
- Boundry value problem
- Principle of superposition
- Eigen value problems
- General forms of first-order linear equations in two variables
- Second-order equations in one independent variable
- Classifiation of second-order linear equations
- Method of seperation of variables
- Strum liouville system (SL-system)
- Sturm liouville (SL) differential operator
- Equation of simple harmonic motion
- Legendre's differential equation
- Bessele's differential equation
- The Hermite equation
- The lagrange equation
- Airy's equation
- Boundary conditions associate with SL system
- Orthogonal function
- Lagrange's identity
- Reality of eigenvalues
- Orthogonality of eigenvalues
- Simplicity of eigenvalues
- Abel's formula
- Completeness of eigenvalues