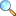MTH424: Convex Analysis (Spring 2024)

At the end of this course the students will be able to understand the concept of Convex Analysis, convex sets, convex functions, Differential of the convex function. Developing ability to study the Hadamard-Hermite inequalities and their applications. Prepare students to be self independent and enhance their mathematical ability by giving them home work and projects.

Convex sets and their properties, Convex hull and their properties, Best approximation theorem. Convex functions, Basic definitions, properties, various generalizations, Differentiable convex functions, Hermite and Hadamard inequalities, Subgradient, Characterizations and applications in linear and nonlinear optimization.

• Assignment 01 | Download PDF | View Online

• Assignment 02 | Download PDF | View Online

• Lectures Handout (Volume 1) | Download PDF | View PDF

Please click on View Online to see inside the PDF.

• http://en.wikipedia.org/wiki/Convex_function
• http://mathworld.wolfram.com/ConvexFunction.html

1. A. W. Roberts and D. E. Varberg, Convex Functions, Academic Press, New York, 1973. (Google Book Preview)
2. Nonlinear Programming Theory and Algorithms, 3rd Edition, by M. S. Bazaraa, H. D. Sherali and C. M. Shetty.
3. Convex Functions and Their Applications, A Contemporary Approach, by C. P. Niculescu and L. E. Persson.
4. Convex Analysis and Monotone Operator Theory in Hilbert Spaces, by H. H. Bauschke and P. L. Combettes.